Semestre 2 2023
Available courses
Today, in the context of significant economic transformations, whether at the national or international level, entrepreneurship plays a crucial role not only in the field of economic and financial studies but also as a practice in our daily lives.
The student of today is the entrepreneur of tomorrow.
Entrepreneurial practice is the future.
This highlights the importance for engineering students in technological sciences to take specialized courses in business economics and entrepreneurship.
The student of today is the entrepreneur of tomorrow.
Entrepreneurial practice is the future.
This highlights the importance for engineering students in technological sciences to take specialized courses in business economics and entrepreneurship.
Course title: Human Engineering 02
Teacher: MOUSSOUNI Soumia
E-mail: soumia.moussouni@g.enp.edu.dz
Target audience: 1st year preparatory cycle, new high school graduates
The Human Engineering module aims to explore the fundamental tools and concepts for analyzing and improving human and professional interactions in various contexts. It emphasizes the application of methodological and ethical approaches tailored to the challenges of the modern work environment.
Module Objectives
Develop methodological skills to analyze and solve human and professional issues.
Strengthen ethical knowledge related to the engineering profession, focusing on social and professional responsibilities.
Enhance personal and professional development by fostering self-management and the evolution of skills within a professional framework.
Teacher: MOUSSOUNI Soumia
E-mail: soumia.moussouni@g.enp.edu.dz
Target audience: 1st year preparatory cycle, new high school graduates
The Human Engineering module aims to explore the fundamental tools and concepts for analyzing and improving human and professional interactions in various contexts. It emphasizes the application of methodological and ethical approaches tailored to the challenges of the modern work environment.
Module Objectives
Develop methodological skills to analyze and solve human and professional issues.
Strengthen ethical knowledge related to the engineering profession, focusing on social and professional responsibilities.
Enhance personal and professional development by fostering self-management and the evolution of skills within a professional framework.
At the core of electrical engineering and physics lies the fundamental principle known as Ohm's Law. This principle elucidates a vital connection between three key elements in an electrical circuit : voltage (V), current (I), and resistance (R). Mathematically expressed as:
V = I × R
Ohm's Law serves as a guiding equation, providing insights into the intricate relationship among these essential parameters. In essence, to grasp the resistance (R) within a circuit, one must simultaneously comprehend the voltage across its terminals (V) and the intensity of the current (I) flowing through it. This foundational concept forms the bedrock of electrical understanding and measurement, shaping the way we analyze and engineer electrical systems.
The mechanics presented here concern exclusively the mechanics of the point.
In practice, it concerns material objects whose spatial extension is very small: their deformations and the energy linked to their own rotational movement can therefore be neglected in comparison with the energies involved. However, an object as voluminous such as the earth or the sun can in some cases be assimilated to a point in terms of its action on bodies in its surroundings, for instance.
Le cours d'algèbre de première année en classes préparatoires aux grandes écoles (CPGE) scientifiques constitue un socle fondamental pour la formation des étudiants en mathématiques. Il couvre plusieurs aspects théoriques de l'algèbre, allant des structures de base aux théorèmes importants, en passant par la résolution de problèmes concrets. Voici les principaux thèmes abordés dans le programme :
1. Structures algébriques fondamentales
Notions de logique mathématique : Assertions, connecteurs logique, quantificateurs.
Ensembles : Notions d'ensembles, sous-ensembles, opérations sur les ensembles, produits cartésiens.
Relations binaires : relation d'équivalence, relation d'ordre.
Applications et fonctions : injections, surjections, bijections, et applications réciproques.
Groupes : Notions de groupe, sous-groupe, groupes abéliens.
Anneaux et corps : Définition des anneaux, corps, propriétés des anneaux commutatifs.
Polynômes : Opérations sur les polynômes, divisions euclidiennes, factorisation, et racines.
2. Espaces vectoriels
Définition et exemples : Notion d’espace vectoriel sur un corps, exemples de ℝ et ℂ, sous-espaces vectoriels.
Bases et dimensions : Bases d’un espace vectoriel, existence de bases, dimension d’un espace vectoriel, rang d'une famille de vecteurs.
Applications linéaires : Définition, noyau, image, théorème du rang, et applications entre espaces de dimensions finies.
3. Matrices et systèmes d'équations linéaires
Définition et opérations : Matrices carrées, transposition, matrices inversibles, et matrices particulières (diagonales, triangulaires).
Résolution des systèmes linéaires : Méthodes de Gauss, matrices augmentées, et interprétation géométrique.
Déterminants : Calcul des déterminants, développement par rapport aux mineurs, et applications aux matrices inversibles.
4. Réduction des endomorphismes et des matrices
Valeurs propres et vecteurs propres : Calcul des valeurs propres et des vecteurs propres, polynôme caractéristique, diagonalisation des matrices.
Réduction de matrices : Diagonalisation et trigonalisation.
1. Structures algébriques fondamentales
Notions de logique mathématique : Assertions, connecteurs logique, quantificateurs.
Ensembles : Notions d'ensembles, sous-ensembles, opérations sur les ensembles, produits cartésiens.
Relations binaires : relation d'équivalence, relation d'ordre.
Applications et fonctions : injections, surjections, bijections, et applications réciproques.
Groupes : Notions de groupe, sous-groupe, groupes abéliens.
Anneaux et corps : Définition des anneaux, corps, propriétés des anneaux commutatifs.
Polynômes : Opérations sur les polynômes, divisions euclidiennes, factorisation, et racines.
2. Espaces vectoriels
Définition et exemples : Notion d’espace vectoriel sur un corps, exemples de ℝ et ℂ, sous-espaces vectoriels.
Bases et dimensions : Bases d’un espace vectoriel, existence de bases, dimension d’un espace vectoriel, rang d'une famille de vecteurs.
Applications linéaires : Définition, noyau, image, théorème du rang, et applications entre espaces de dimensions finies.
3. Matrices et systèmes d'équations linéaires
Définition et opérations : Matrices carrées, transposition, matrices inversibles, et matrices particulières (diagonales, triangulaires).
Résolution des systèmes linéaires : Méthodes de Gauss, matrices augmentées, et interprétation géométrique.
Déterminants : Calcul des déterminants, développement par rapport aux mineurs, et applications aux matrices inversibles.
4. Réduction des endomorphismes et des matrices
Valeurs propres et vecteurs propres : Calcul des valeurs propres et des vecteurs propres, polynôme caractéristique, diagonalisation des matrices.
Réduction de matrices : Diagonalisation et trigonalisation.
algorithmique et langage c
Instructor : Dr. Morsli Mohamed
Email : mohamed.morsli@g.enp.edu.dz
Target Audience : First-year preparatory cycle students
The importance of economics for students of the National Polytechnic School : The economy plays a very important role in people’s lives, so the study of this science and the changing economic phenomena is no longer limited to specialists, but has become central to all different specializations, including students of the National Polytechnic School (considering them the leaders of the future).
Unit 1: Climate Change
Text: Save the Bees
Video: Planet Plastic
Lesson Aims: Speaking about some of the most endangered animals and species in our
world.
Identifying problems and suggesting solutions.
Producing a poster about an endangered animal or species: introducing the
animal and stating why it is in danger, listing its problems, listing suggested
solutions for its problems, and closing the poster with a call-to-act.
Language points:
1. Language: Conditionals
2. Language Structure: Making suggestions.
Text: Save the Bees
Video: Planet Plastic
Lesson Aims: Speaking about some of the most endangered animals and species in our
world.
Identifying problems and suggesting solutions.
Producing a poster about an endangered animal or species: introducing the
animal and stating why it is in danger, listing its problems, listing suggested
solutions for its problems, and closing the poster with a call-to-act.
Language points:
1. Language: Conditionals
2. Language Structure: Making suggestions.
Course title: Human Engineering 01
Teacher: MOUSSOUNI Soumia
E-mail: soumia.moussouni@g.enp.edu.dz
Target audience: 1st year preparatory cycle, new high school graduates
Autonomous or guided monitoring: guided
Objectives of the Human Engineering Module:
Teacher: MOUSSOUNI Soumia
E-mail: soumia.moussouni@g.enp.edu.dz
Target audience: 1st year preparatory cycle, new high school graduates
Autonomous or guided monitoring: guided
Objectives of the Human Engineering Module:
- Enterprise and Organizational Structure: Analyze different types of enterprises and organizational structures, evaluating their impact on performance and workplace dynamics.
- Corporate Culture: Examine how organizational culture influences employee behavior, motivation, and strategic alignment within businesses.
- Corporate Communication: Develop advanced skills in interpersonal and organizational communication to optimize the flow of information and enhance interdisciplinary collaboration.
- Sustainable Growth : Integrate the principles into the design and implementation of organizational practices, considering societal and environmental challenges.
- Collective Actions: Promote employee engagement and participation in collective initiatives aimed at achieving strategic organizational objectives, reinforcing shared leadership and collective responsibility.
Les circuits électriques sont devenus une partie tellement indispensable de notre quotidien qu'on ne fait même plus attention à toute la complexité de ce qu'il y a derrière le simple fait d'allumer une lampe dans son salon ou son téléviseur ou le feu clignotant de son véhicule, ou encore le fait de démarrer le moteur de ce dernier.
Tous les systèmes énumérés ci-dessus ne sont en fait que des systèmes électriques plus ou moins complexes et composés essentiellement d'éléments de base des circuits électriques.
Tous les systèmes énumérés ci-dessus ne sont en fait que des systèmes électriques plus ou moins complexes et composés essentiellement d'éléments de base des circuits électriques.
Les vibrations sont des oscillations qui se propagent à travers un milieu, qu'il soit solide, liquide ou gazeux. Elles se manifestent sous diverses formes, allant des ondes sonores que nous entendons dans l'air aux vibrations que l'on peut ressentir lorsqu'on touche un objet en mouvement. En physique, les vibrations sont souvent décrites par leur fréquence, leur amplitude et leur forme d'onde. Elles jouent un rôle crucial dans de nombreux domaines, de la musique et l'ingénierie à la médecine et la technologie. Comprendre les vibrations nous permet de mieux saisir les phénomènes naturels et d'améliorer les dispositifs technologiques qui en dépendent.
L'analyse numérique est une discipline à l'interface des mathématiques et de l'informatique. Elle s'intéresse tant aux fondements qu'à la mise en pratique des méthodes permettant de résoudre, par des calculs purement numériques, des problèmes d'analyse mathématique.
Ce cours est destiné à des étudiants de 2ème année de licence en technologie . Il est souhaitable pour le suivre dans de bonnes conditions d'avoir quelques pré-requis en algèbre, en structure des ordinateurs et éventuellement en programmation structurée (langage C).
Ce cours est destiné à des étudiants de 2ème année de licence en technologie . Il est souhaitable pour le suivre dans de bonnes conditions d'avoir quelques pré-requis en algèbre, en structure des ordinateurs et éventuellement en programmation structurée (langage C).
La chimie est une science de la nature qui étudie la matière et des transformations et plus précisément les atomes, les molécules et les différents types de réaction chimique.
La résistance des matériaux est un domaine de l'ingénierie qui étudie les propriétés mécaniques
des matériaux (la dureté, la ductilité, la fragilité, l'élasticité, la plasticité, la résistance à la fatigue, la résistance à la corrosion, etc.), et les méthodes utilisées pour les analyser et les calculer la mécanique rationnelle à la compréhension des forces et des déformations sur une structure, tandis que la résistance des matériaux s'occupe de l'étude des propriétés et comportements des matériaux utilisés dans cette structure).
La RDM vise à comprendre comment les matériaux réagissent aux charges et à développer des compétences pour les utiliser de manière efficace dans la conception de structures et de machines.
Le but des TP RDM est de comprendre comment les matériaux réagissent aux charges et de développer des compétences pour les utiliser de manière efficace dans la conception de structures et de machines, ainsi de trouver les propriétés mécaniques des matériaux.
a. Essai destructif
b. Essai non destructif ite.
Les travaux pratique que vous allez étudier sont les suivants :
- Essai de traction (Compression)
- Essai de flexion
- Essai de torsion
des matériaux (la dureté, la ductilité, la fragilité, l'élasticité, la plasticité, la résistance à la fatigue, la résistance à la corrosion, etc.), et les méthodes utilisées pour les analyser et les calculer la mécanique rationnelle à la compréhension des forces et des déformations sur une structure, tandis que la résistance des matériaux s'occupe de l'étude des propriétés et comportements des matériaux utilisés dans cette structure).
La RDM vise à comprendre comment les matériaux réagissent aux charges et à développer des compétences pour les utiliser de manière efficace dans la conception de structures et de machines.
Le but des TP RDM est de comprendre comment les matériaux réagissent aux charges et de développer des compétences pour les utiliser de manière efficace dans la conception de structures et de machines, ainsi de trouver les propriétés mécaniques des matériaux.
a. Essai destructif
b. Essai non destructif ite.
Les travaux pratique que vous allez étudier sont les suivants :
- Essai de traction (Compression)
- Essai de flexion
- Essai de torsion
Dr. Houda BAGHLI / Process and chemical engineering
Here are the objectives of the course Chemical Engineering as a Systems Engineering Discipline:1. Understand the Role of Chemical Engineering in Society
o Explore how chemical engineering contributes to improving the quality of life and addresses the demands of the 21st century.
2. Learn the History and Evolution of Chemical Engineering
o Gain insight into the development of the field and its major contributions to society over time.
3. Understand the Principles of Chemical Engineering Design
o Study the foundational principles and their applications in creating sustainable and innovative solutions.
4. Analyze and Solve Problems in Chemical and Allied Industries
o Learn how to use modern techniques, engineering tools, and simulation methodologies to address industry challenges.
5. Explore Sustainable Development
o Understand the importance of sustainability, life-cycle analysis, and environmental impact mitigation in chemical engineering processes.
6. Foster Safety Awareness
o Recognize the significance of safety principles and practices in process industries.
7. Enhance Multidisciplinary Collaboration and Leadership Skills
o Develop teamwork, leadership, and communication skills to work effectively in professional environments.
8. Learn Professional and Ethical Responsibilities
o Understand the ethical standards required for responsible engineering practice.
9. Engage in Lifelong Learning and Innovation
o Foster a mindset of continuous improvement to stay updated with modern advancements in the field.
10. Explore Career Opportunities and Professional Orientation
o Gain insights into the various fields and career paths in chemical engineering, along with an understanding of its methodologies and computational tools.
These objectives aim to provide you with a holistic understanding of chemical engineering and prepare you for professional and academic success in the field.
Unité transversale (enseignement des techniques de communication et d'expression en langue française.)
The distant courses are intended for 2nd year Preparatory school students.
Département: Preparatory cycle
Level : 2nd year
Name of the lecture : AST3/AST4
Crédit:01 Coefficient:01
Durée : 15 semaines
Horaire: Mardi: 09h30-11h00 Salle: F09
Enseignant : Cours, TD et TP: Dr. BOUAYED Maliha
Contact : maliha.bouayed@g.enp.edu.dz
availability :
In the office 'English Cell' (New Admin.block, 3rd floor) : Sunday 9a.m-13h30
Wednesday : 9a.m-13h30
Dark matter is a hypothesized form of matter that is not visible and is believed to constitute the majority of the total matter in the Universe. Although it possesses mass, it remains undetectable and does not engage with conventional matter.
Travaux Pratiques : TP_Analyse Numérique 2
Auteur : Dr. LEILA BENACHOUR
Grade : Maitre Assistante Classe B
Public Ciblé : 2ème Année Tronc commun Classes Préparatoires.
Département : Classes Préparatoires.
Établissement : École Nationale Polytechnique ENP, El Harrach. Alger.
Les Travaux Pratiques Analyses Numériques (TP_ANA_NUM2) sont dirigés aux étudiants de 2éme Année Tranc Commun à l’ENP est élaboré dans le cadre de la Formation Pédagogique de Constantine des TIC visant les enseignants nouvellement recrutés.
Ils rassemblent un certain nombre de méthodes numériques étudiées dans les différents chapitres du cours d’analyses numériquesL'électricité générale est une branche fondamentale de la physique qui étudie les phénomènes électriques et leurs applications dans différents domaines. Elle forme la base de nombreuses technologies modernes et est essentielle à notre vie quotidienne. L'étude de l'électricité générale comprend plusieurs aspects, notamment les charges électriques, les courants électriques, les champs électriques et magnétiques, ainsi que les circuits électriques.
This course will introduce you to various techniques used in chemistry laboratory as well as procedures and some methods of identification of chemical compounds.
The contents of this course material illustrate important concepts and principles in general chemistry. Three basic goals guided the development of all experiments in this material:
the experiments illustrate the concepts learned in the classroom; (2) the experiments are clearly and concisely written so that students will easily understand the task at hand, will work with minimal because the manual provides enough information on experimental procedures, and will be able to perform the experiments in 3 hour laboratory period; and (3) the experiments are not only simple demonstrations, but also contain a sense of discovery. In addition, laboratory safety tips as well as common laboratory techniques are explored. Practicals in chemistry 1 consists of three units that : Unit I in the course introduce you to laboratory safety rules, common laboratory apparatus and a series of detailed instructions and explanations dealing with the basic laboratory techniques of chemistry. Unit II contains experiments that introduce you to the techniques used in the preparation of solutions. Unit III consist of experimental method for the determination values of the wavelength of the atoms by atomic spectra using a diffraction grating.
L'analyse numérique est une branche des mathématiques qui se concentre sur les méthodes pour obtenir des solutions numériques à des problèmes mathématiques. Ce module d'analyse numérique est conçu pour vous fournir une compréhension approfondie de ces méthodes et de leur application à divers problèmes.
Dans ce module, vous allez explorer plusieurs techniques d'approximation numérique, y compris l'interpolation, la dérivation, l'intégration, et la résolution d'équations non linéaires. Chaque chapitre du module se concentre sur une technique spécifique, en commençant par une introduction théorique suivie d'exemples pratiques pour illustrer l'application de la technique.
L'objectif de ce module est de vous fournir les outils nécessaires pour résoudre des problèmes mathématiques complexes qui ne peuvent pas être résolus exactement avec des méthodes analytiques. À la fin de ce module, vous devriez être capable d'appliquer ces techniques à une variété de problèmes dans des domaines tels que l'ingénierie, la physique, l'économie, et plus encore.
Il est important de noter que l'analyse numérique n'est pas seulement une question de calculs, mais aussi de comprendre comment et pourquoi ces méthodes fonctionnent. Par conséquent, une partie importante de ce module sera consacrée à l'étude des erreurs numériques et à la manière de les minimiser.
En somme, ce module d'analyse numérique est une étape essentielle pour tout étudiant en sciences ou en ingénierie qui souhaite maîtriser les techniques numériques nécessaires pour résoudre des problèmes mathématiques dans le monde réel. Bonne chance avec vos études !
Travaux Pratiques : Analyse Numérique 2
Auteur : Dr. ABADA ZAKARIA
Grade : Maitre assistante Classe B
Public Ciblé : 2ème Tronc commun Année Classes Préparatoires.
Département : Classes Préparatoires.
Établissement : École Nationale Polytechnique ENP, El Harrach. Alger.
résumé du cours :
Ce cours aborde les notions d'erreurs et les systèmes d'équations non linéaires. Dans le premier chapitre, on définit l'erreur absolue et relative, en distinguant les erreurs de mesure, de méthode, et d'arrondi, ainsi que leur propagation dans les calculs. Le deuxième chapitre se concentre sur les méthodes de résolution des systèmes d'équations non linéaires, en présentant la méthode de dichotomie, qui divise un intervalle pour trouver une racine, et la méthode de Newton-Raphson, qui utilise des dérivées pour une convergence rapide. La dichotomie est simple et robuste, tandis que Newton-Raphson est plus efficace mais nécessite une bonne estimation initiale. Ces outils sont essentiels pour la modélisation et la résolution de problèmes complexes en mathématiques appliquées.
Auteur : Dr. ABADA ZAKARIA
Grade : Maitre assistante Classe B
Public Ciblé : 2ème Tronc commun Année Classes Préparatoires.
Département : Classes Préparatoires.
Établissement : École Nationale Polytechnique ENP, El Harrach. Alger.
résumé du cours :
Ce cours aborde les notions d'erreurs et les systèmes d'équations non linéaires. Dans le premier chapitre, on définit l'erreur absolue et relative, en distinguant les erreurs de mesure, de méthode, et d'arrondi, ainsi que leur propagation dans les calculs. Le deuxième chapitre se concentre sur les méthodes de résolution des systèmes d'équations non linéaires, en présentant la méthode de dichotomie, qui divise un intervalle pour trouver une racine, et la méthode de Newton-Raphson, qui utilise des dérivées pour une convergence rapide. La dichotomie est simple et robuste, tandis que Newton-Raphson est plus efficace mais nécessite une bonne estimation initiale. Ces outils sont essentiels pour la modélisation et la résolution de problèmes complexes en mathématiques appliquées.
Intitulé de la Matière : TP. Physique 3 , Unité d’enseignement : Fondamentale UEF212, Code : PHY3, Semestre : 03, Crédit : 04 , Coefficient : 04, Public cible : 2 ème Année, Cycle Préparatoire.
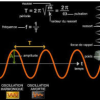
Les vibrations ou oscillations des systèmes représentent l'un des domaines d'étude les plus importants en physique. En effet, les vibrations apparaissent lorsque le système est dévié de sa position d'équilibre à cause d’une énergie fournie par une source externe. Une force de stockage, ou une force conservatrice, souvent associée à une composante d'énergie potentielle comme un ressort, agit pour ramener le système vers sa position d'équilibre. Les principaux objectifs de l'étude des vibrations sont de comprendre leur impact sur la performance et la sécurité des systèmes, ainsi que de contrôler leurs effets.
Le cours constitue la première partie du programme de la matière « Vibrations et Ondes », enseignée en deuxième année des classes préparatoires Intégrées.Il vise à fournir aux étudiants une compréhension fondamentale des mouvements vibratoires
Instructor : Dr. Morsli Mohamed
Email : mohamed.morsli@g.enp.edu.dz
Target Audience : First-year preparatory cycle students
The importance of economics for students of the National Polytechnic School : The economy plays a very important role in people’s lives, so the study of this science and the changing economic phenomena is no longer limited to specialists, but has become central to all different specializations, including students of the National Polytechnic School (considering them the leaders of the future).
Skip course categories